Что такое египетский треугольник? - ответы на вопросы про технологии и не только

Полезно вспомнить

Треугольник

Треугольник прямолинейный, часть плоскости, ограниченная тремя отрезками прямых (стороны Треугольника (в геометрии)), имеющими попарно по одному общему концу (вершины Треугольника (в геометрии)). Треугольник, у которого длины всех сторон равны, называется равносторонним, или правильным, Треугольник с двумя равными сторонами — равнобедренным. Треугольник называется остроугольным, если все углы его острые; прямоугольным — если один из его углов прямой; тупоугольным — если один из его углов тупой. Более одного прямого или тупого угла Треугольник (в геометрии) иметь не может, так как сумма всех трёх углов равна двум прямым углам (180° или, в радианах, p). Площадь Треугольник (в геометрии) равна ah/2, где а — любая из сторон Треугольника, принимаемая за его основание, a h — соответствующая высота. Стороны Треугольника подчинены условию: длина каждой из них меньше суммы и больше разности длин двух других сторон.

Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки.

Трём точкам пространства, не лежащим на одной прямой, соответствует одна и только одна плоскость.
Любой многоугольник можно разбить на треугольники — этот процесс называется триангуляция.
Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Типы треугольников

По виду углов

Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:

Если все углы треугольника острые, то треугольник называется остроугольным;
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.

По числу равных сторон

Разносторонним называется треугольник, у которого длины трёх сторон попарно различны.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.

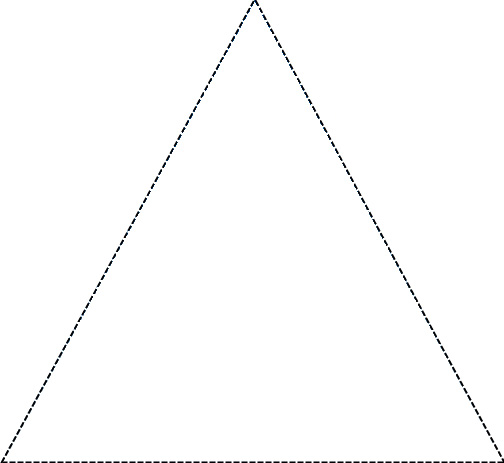
Правильный

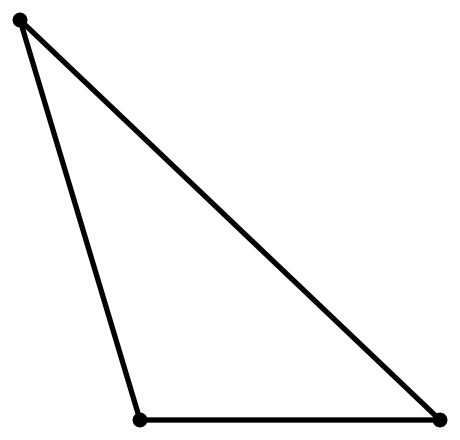
Тупоугольный’

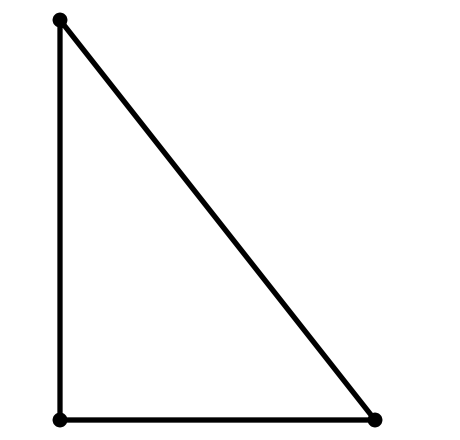
Прямоугольный

Разносторонний

Равнобедренный

Равносторонний

Остроугольный

Как можно улучшить свои результаты в торговле треугольников?

Первая и самая важная вещь — это таймфреймы, которые вы будете использовать. Держитесь подальше от низких таймфреймов и внутридневного шума, который может возникнуть в результате незначительных новостных событий и случайных колебаний цены. Также на более старших таймфреймах ложные пробои гораздо более редки.

У вас появится гораздо больше времени для принятия торговых решений. Вы будете меньше волноваться и сможете спокойно найти оптимальную точку входа и определиться с целями по взятию прибыли.

Заключайте меньшее количество сделок. Если вы торгуете по дневным таймфреймам и совершаете более десяти сделок в месяц, существует 90% вероятность, что вы торгуете слишком часто. Другими словами, вы выбираете количество, а не качество. Когда речь заходит о лучших точках входа — их всегда будет не так много. По моему опыту, это число колеблется от трех- четырех до, возможно, десяти в течение активного месяца.

Прежде чем добавлять треугольник в свой торговый арсенал, вам придется набраться терпения. Не ожидайте появления этой фигуры каждую неделю или даже каждый месяц. Однако при правильном соотношении риска к прибыли потенциальный доход может оправдать все ваши ожидания.

Постоянно отслеживайте свои результаты, как хорошие, так и плохие. Отслеживать свои ошибки гораздо важнее, чем ваши успехи. Несмотря на то, что иногда это утомительно и даже скучно, ведение торгового журнала является решающим шагом для становления прибыльного трейдера.

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

все стороны и площадь состоят из целых чисел, как говорилось выше;
согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Египетский треугольник

Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3:4:5. Особенностью треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины.

Название треугольнику с таким отношением сторон дали эллины. В VII — V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к формулировке и доказательству его знаменитой теоремы.

Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Примеры треугольника Карпмана в жизни

Нужно отметить, что треугольник Карпмана встречается и в реальной жизни, причем очень часто. Вполне возможно, что вы сами являетесь его частью. Попробуйте провести анализ взаимоотношений с людьми, которые вас окружают.

Классическим примером треугольника Карпмана является семья, где мама, папа и ребенок постоянно меняются ролями. Малыш, до того момента, пока не достиг возраста, когда он уже разумно себя ведет, является «Тираном», которому необходима «Жертва», чтобы она исполняла его желания, самоутверждения и потребности.

Читать ›

Если в какой-то момент избалованного ребенка не сместили с этой роли, он может и дальше самоутверждаться за счет своих родителей, чаще всего матери. Отец в данном случае выступает в роли «Спасателя», который вроде старается оказать помощь, однако единственное, что у него получается, это тоже самоутверждаться за счет жены, проявляя к ней сочувствие.

Если же глава семьи обладает авторитарным характером, то «Жертвой» становятся дети или жена. Не получившие эту роль – беспомощные «Контролеры» («Свидетели»). Чаще всего это теща или свекровь, которые настраивают супругов друг против друга, в первом случае жену против мужа, во втором – наоборот.

Ярким примером «Спасителей» являются лучшие подруги, которые, как теща или свекровь, жалеют «Жертву» (плохого парня, бойфренда), повышая собственную самооценку и чувство собственной важности.

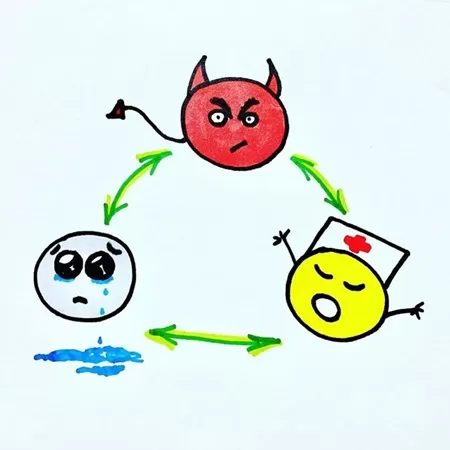
Если говорить о коллективах, то в них «Тираном» чаще всего является руководитель, а «Жертвы» – это некоторые сотрудники. При этом не всегда положение тех, кому кажется, что их унижают, является соответствующим действительности. Если у человека есть склонность к психологии «Жертвы», то он всегда будет искать момент, чтобы занять положение, которое для него привычно.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом , так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

Применение египетского треугольника

В Древние века в архитектуре и строительстве египетский треугольник пользовался огромной популярностью. Особенно он был необходим, если для построения прямого угла использовали веревку или шнур.

Ведь известно, что отложить прямой угол в пространстве, является довольно таки сложным занятием и поэтому предприимчивые египтяне изобрели интересный способ построения прямого угла. Для этих целей они брали веревку, на которой отмечали узелками двенадцать ровных частей и потом с этой веревки складывали треугольник, со сторонами, которые равнялись 3 , 4 и 5 частям и в итоге без проблем, получали прямоугольный треугольник. Благодаря такому замысловатому инструменту, египтяне с огромной точностью размеряли землю для сельскохозяйственных работ, строили дома и пирамиды.

Вот так посещение Египта и изучение особенностей египетской пирамиды подтолкнуло Пифагора на открытие своей теоремы, которая, кстати, попала в Книгу Рекордов Гиннеса, как теорема, которая имеет самое большое количество доказательств.

Треугольные колеса Рело

Колесо
— круглый (как правило), свободно вращающийся или закреплённый на оси диск, позволяющий поставленному на него телу катиться, а не скользить. Колесо повсеместно используется в различных механизмах и инструментах. Широко применяется для транспортировки грузов.

Колесо существенно уменьшает затраты энергии на перемещение груза по относительно ровной поверхности. При использовании колеса работа совершается против силы трения качения, которая в искусственных условиях дорог существенно меньше, чем сила трения скольжения. Колёса бывают сплошные (например, колёсная пара железнодорожного вагона) и состоящие из довольно большого количества деталей, к примеру, в состав автомобильного колеса входит диск, обод, покрышка, иногда камера, болты крепления и тд. Износ покрышек автомобилей является почти решённой проблемой (при правильно установленных углах колёс). Современные покрышки проезжают свыше 100 000 км
. Нерешённой проблемой является износ покрышек у колёс самолётов. При соприкосновении неподвижного колеса с бетонным покрытием взлётной полосы на скорости в несколько сотен километров в час износ покрышек огромен.

В июле 2001 года на колесо был получен инновационный патент со следующей формулировкой: «круглое устройство, применяемое для транспортировки грузов». Этот патент был выдан Джону Кэо, юристу из Мельбурна, который хотел тем самым показать несовершенство австралийского патентного закона .
Французская компания Мишлен в 2009 году разработала пригодное к массовому выпуску автомобильное колесо Active Wheel со встроенными электродвигателями, приводящими в действие колесо, рессору, амортизатор и тормоз. Таким образом, эти колёса делают ненужными следующие системы автомобиля: двигатель, сцепление, коробку передач, дифференциал, приводной и карданный валы.
В 1959 году американец А. Сфредд получил патент на квадратное колесо. Оно легко шло по снегу, песку, грязи, преодолевало ямы. Вопреки опасениям, машина на таких колёсах не «хромала» и развивала скорость до 60 км/ч.

Франц Рело
(Franz Reuleaux, 30 сентября 1829 — 20 августа 1905) — немецкий инженер-механик, лектор Берлинской Королевской Технической академии, ставший впоследствии ее президентом. Первым, в 1875 году, разработал и изложил основные положения структуры и кинематики механизмов; занимался проблемами эстетичности технических объектов, промышленным дизайном, в своих конструкциях придавал большое значение внешним формам машин. Рело часто называют отцом кинематики.

Разметка под фундамент своими руками

Качество постройки в огромной степени зависит от того, насколько правильно была выполнена разметка под фундамент

Занимаясь этой работой важно с максимальной точностью выдержать все прямые углы. Разметка фундамента своими руками под частный дом может быть выполнена несколькими способами. Чаще всего используются метод «египетского» треугольника и метод двух кривых

Поэтому в этой статье рассмотрим именно их

Чаще всего используются метод «египетского» треугольника и метод двух кривых. Поэтому в этой статье рассмотрим именно их.

Какие инструменты понадобятся?

Производится разметка фундамента своими руками с применением инструментов:

Рулетки;
Шнура;
Гидроуровня и отвеса;
Помимо этого понадобятся деревянные колышки.

С чего начать разметку?

Итак, как провести разметку фундамента? Для начала следует определить две исходные точки, вбив колышки по углам будущего здания, находящимся на одной прямой со стороны его самой длинной стены. Далее от них нужно будет провести перпендикуляры, таким образом отметив внешний контур смежных стен.

«Египетский треугольник». Самый простой метод

Разметка фундамента своими руками быстрее всего может быть произведена методом «золотого» треугольника, имеющего соотношение длин сторон 5*3*4. Мероприятие при этом выполняется в несколько этапов:

1. Для начала нужно найти длинную веревку и завязать на ней четыре узла. Первый – на конце, второй на расстоянии 3м, третий в четырех метрах от второго и последний в пяти метрах от третьего; 2. После этого самый первый и самый последний узлы соединяют гвоздем. По гвоздю следует вбить и в каждый из промежуточных узлов; 3. При этом длинную сторону получившегося треугольника нужно расположить вдоль линии между двумя уже вбитыми колышками; 4. Вдоль короткой стороны проводят требуемый перпендикуляр; 5. На полученной прямой, вбивают третий колышек на расстоянии равном ширине здания.

Важно: Правильность всех замеров следует обязательно проверить. Для этого между вбитыми кольями по диагоналям натягивают два шнура и связывают в месте пересечения

Paste a VALID AdSense code in Ads Elite Plugin options before activating it.

Метод двух дуг

Разметка фундамента своими силами этим методом выполняется также с использованием веревки. Предварительно от одного из колышков в обе стороны по уже имеющейся прямой отмеряют равные расстояния и отмечают найденные места. Далее к одной из полученных точек прикрепляют веревку с привязанным на противоположном конце гвоздем. Натянув ее проводят дугу напротив того колышка, от которого отмерялись расстояния. Затем веревку крепят ко второму отмеченному месту и чертят еще одну дугу. Из той точки, где дуги пересекутся, проводят линию к колышку. В результате получается прямой угол между ней и уже имеющейся линией.

На заключительном этапе к кольям на высоте будущего фундамента привязывают шнур, поверяя горизонтальность его положения со всех четырех сторон, пользуясь строительным уровнем. Для ленточного фундамента чертят внутренний контур параллельно найденному внешнему и также натягивают шнур.

Совет: В том случае, если траншею предполагается копать с привлечением техники, шнуры лучше не использовать. В процессе работы они могут порваться. Линии между найденными точками в этом случае стоит прочертить песком. Для нахождения центров столбов столбчатого фундамента, от найденных углов вдоль прочерченных линий отмеряют необходимые расстояния и ставят отметки. Далее проверяют прямоугольность углов, получившихся на пересечении линий (соединяющей полученные точки на противоположных сторонах и линии периметра, на которой расположены отметки).

Разметка фундамента своими руками, как можно было заметить – процедура не такая уж и сложная. Самое главное, делать все аккуратно, хорошо натягивать веревку и обязательно проверять полученный результат методом диагоналей.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Стороны конструкции имеют следующее соотношение друг к другу:

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять

В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть

Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках